Lupine Publishers | On some Derivatives of Vector-Matrix Products Useful for Statistics

Lupine Publishers- Biostatistics and Biometrics Open Access Journal

 

Mini Review

In this brief description, we will use the numerator layout [1], and will tacitly assume that all products are conformable.
The derivative of the linear form 𝒰^t𝒱 with respect to the vector 𝒱is given as
and since 𝒰^t𝒱 is a scalar, we are facing a particular case of the derivative of a scalar λ with respect to a vector, e.g., ∂_𝒱λ=(∂_𝒱1λ ..... ∂_𝒱nλ) and it must also be ∂_𝒱(𝒰^t𝒱)=∂_𝒱(𝒱^t𝒰) . Moreover, it is easy to demonstrate that using the denominator layout, the derivative would have been ∂_𝒱(𝒰^t𝒱)=𝒰
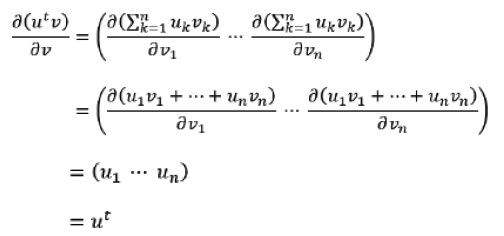
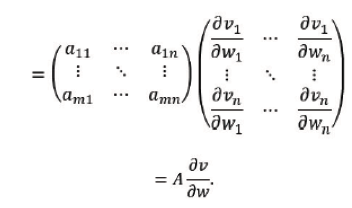
If both 𝒰 and 𝒱 vectors are function of a third vector 𝒵, we get
which, in the case 𝒰=𝒱=𝒲 reduces to
Dealing with a linear transform 𝒰=a𝒱, if A is 𝓂×𝓂 we have
and if 𝒱 is a function of a vector 𝒲_𝒱 we get
From definition of bilinear form, we obtain, for 𝒰^tA𝒱 the derivative
while, for a quadratic form 𝒰^tA𝒱(where A is 𝓃 × 𝓃), we get
so that, if A is a symmetric matrix, say, for A = X^tX, then

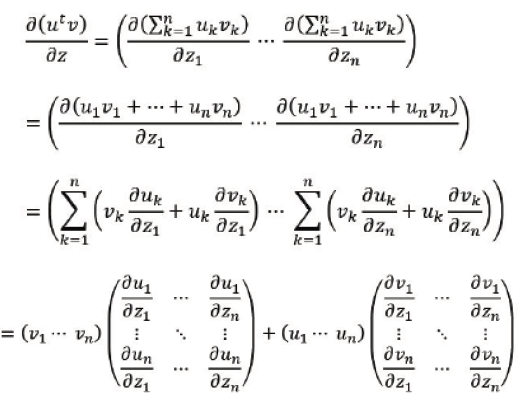
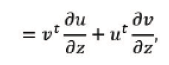
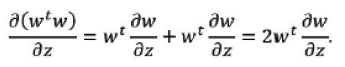
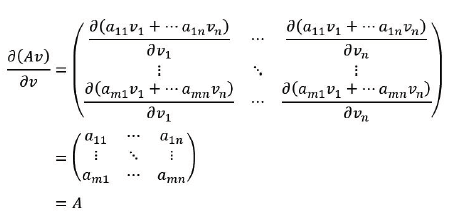
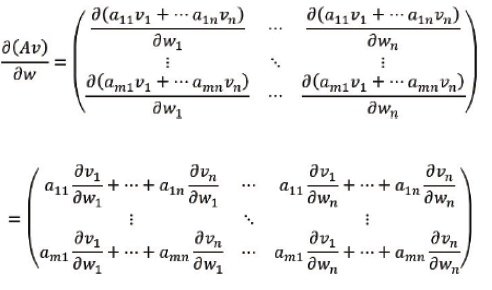
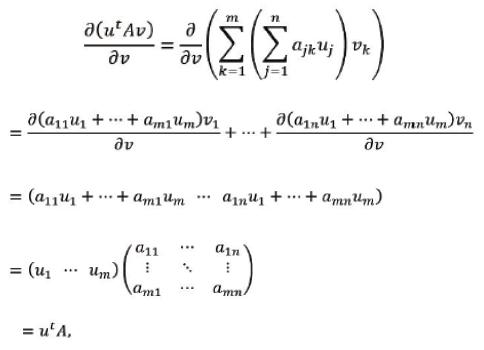
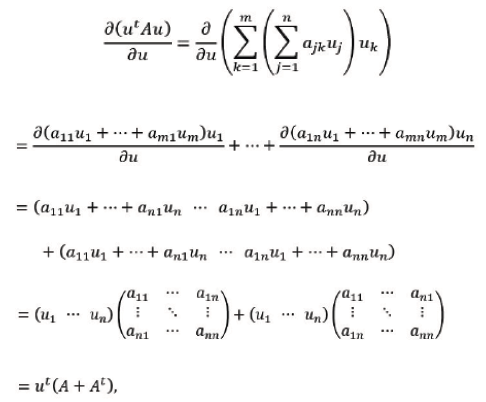
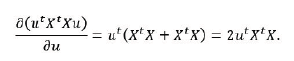
For more Lupine Publishers Open Access Journals Please visit our website:

https://lupinepublishers.us/

For more Bio statistics and Bio metrics Open Access Journal articles Please Click Here:  https://lupinepublishers.com/biostatistics-biometrics-journal/

To Know More About Open Access Publishers Please Click on Lupine Publishers

Follow on Linkedin : https://www.linkedin.com/company/lupinepublishers
Follow on Twitter   :  https://twitter.com/lupine_online